Machine Learning - 給自己的機器學習筆 - Logistic Regression邏輯迴歸 - 二元分類問題 - 原理詳細介紹

1. 邏輯迴歸 Logistic Regression 是什麼?
- 目的: 處理二元分類問題的方式子,也就是Yes or No的二元問題少年,它屬於線性分類器的一種
- 舉例:
- 我會不會錄取
- 公司會不會上市
- 他會不會參加
- 股票會不會漲
- 優缺點:
- 優點: 容易理解與實作,計算成本不高
- 缺點: 分類的準確度不高興,容易產生低度擬和的問題
2. Logistic Regression 與 Linear Regression 的區別? 迴歸可以用在分類問題?
一般的狀況來說快,迴歸與分類是兩種不同的分類預測方式子,迴歸屬於連續型的模型,也就是說迴歸一般不會用在分類問題上,但如果硬要使用它來處理分類問題少年,就會使用邏輯迴歸 - Logistic Regression
處理問題上的區別:
- Linear Regression 線性迴歸屬於連續型的模型值,也就是預測一個連續的應變數
- Logistic Regression 邏輯迴歸使迴歸可以用來處理二元分類問題
建立迴歸方程式的區別
- Linear Regression 線性迴歸使用特徵對目標直接建立迴歸方程式
- Logistic Regression邏輯迴歸對勝算比(Odds Ratio),也就是對與不對的比率,取對數log來建立迴歸方程式
3. Logistic Regression原理
計算步驟
STEP1: 計算Logit(Odds),勝算比取對數log,產生y值
STEP2: 經過函數轉換器,像是Sigmoid函數、Arctan(X)等等
STEP3: 將y值帶入函數轉換公式化,並產生最終結果(介於0~1的數值,> 0.5 表示有勝算比,< 0.5 表示沒勝算)比,大於50%機率的會被預測為1,小於50%會被預測為0
如何計算Logit(Odds)?
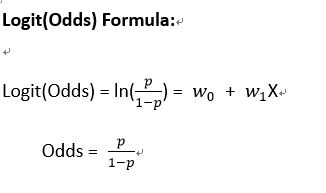
Odds : 勝算比
logit : 取對數
p : 發生的機率
重要提醒
公式的右邊是我另一篇介紹關於Linear Regression裡面的Simple Linear Regression簡單線性迴歸公式化,當然還有Polynomial Regression多項式迴歸、Multivariable Regression多元迴歸等等的公式可以使用,大家可以根據需求調整右邊的迴歸公式喔
函數轉換與產生最終的結果
1. 函數轉換的目的
Logit(Odds)計算出來的結果不一定會介於0~1之間,但是機率不可能小於0,也一定不會大於100%,所以我們要透過函數轉換來將Logit(Odds)計算出來的值轉換成0~1之間的值
2. Sigmoid Function
公式計算
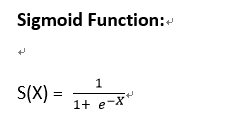
產生的結果
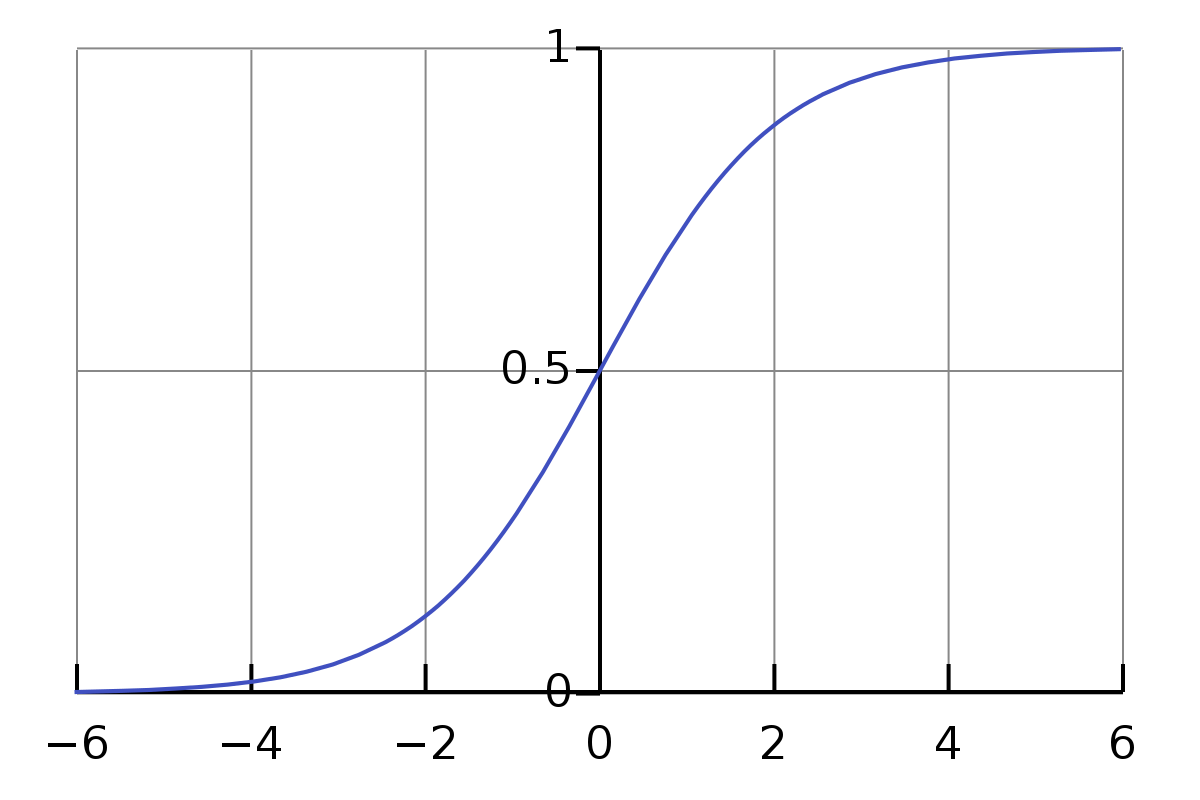
3. Arctan(X)
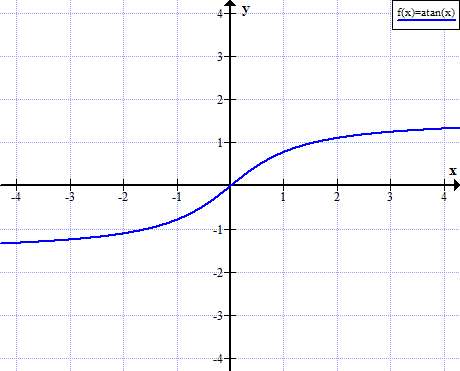
4. 轉換函數的選擇
符合條件
- 遞增
- 計算出來的值介於0~1之間
- 中間遞增的斜率要盡量大(目的是讓機率趨近於0%或100%)
只要滿足上面的條件,就能當成轉換函數使用,當然預測效果的好壞就要透過實驗才知道囉
4. 實際舉例
- 數據集介紹
這邊有一組我自行捏造的數據集,說明了學生花在小考上的讀書時間與最終是否通過考試的數據
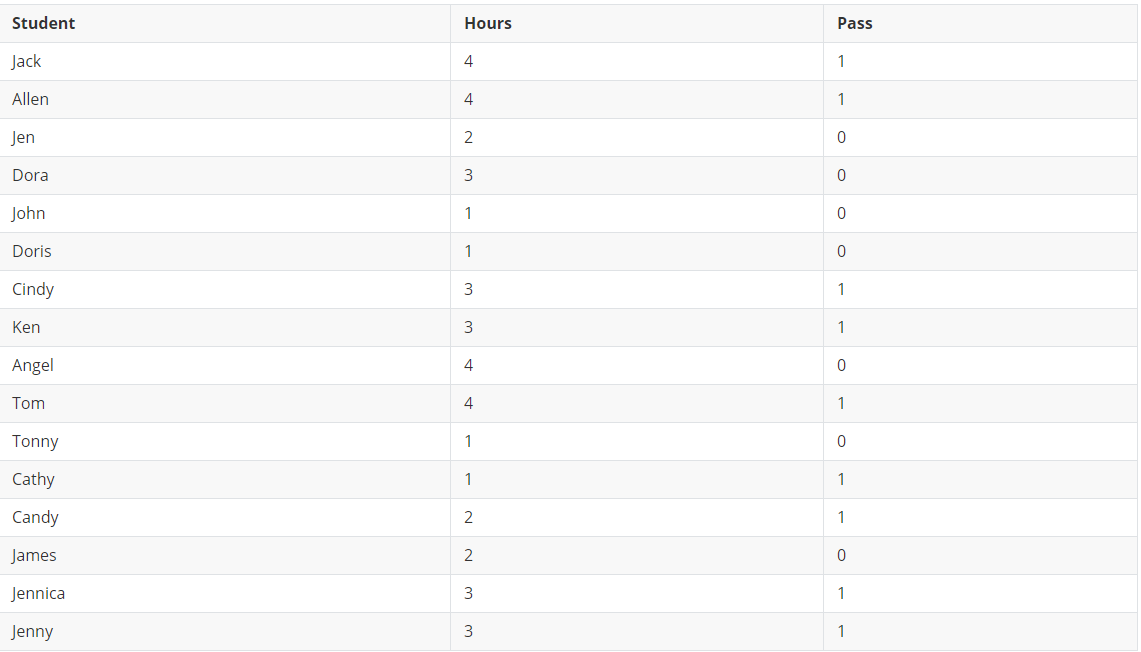
- 計算Logit(Odds)

- 經過Sigmoid轉換
將logit(Odds)結果帶入Sigmoid函數
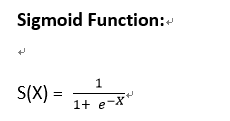
- 結果
計算出介於0~1之間的機率值,大於50%的機率會被預測為1,也就是有通過小考上,小於50%的預測為0,也就是沒有通過小考
5. 邏輯迴歸 Logistic Regression 可以實現多元分類嗎?
- 邏輯迴歸 Logistic Regression 主要處理二元分類問題,但如果真的想處理多元分類問題,可以結合多個二元分類的邏輯迴歸模型達成
- 其實簡單來說就是,假設我們數據集有N個類別,我們先將A類當成一類,其餘所有類別當成一類,以此類推薦,綜合這些倆倆分類問題,就能實現多元分類
結論
邏輯迴歸 Logistic Regression 屬於分類器,就是計算數據的Odds並取對數後,做線性迴歸一,再經由Sigmoid函數將Logit(Odds)計算出來的值轉換成機率(介於0~1之間的值),由於這種轉換函數中間是嚴格要求遞增的,所以計算出來的值會趨近於0(0%)或1(100%),來預測二元分類問題(是與不是)
學會了邏輯迴歸 Logistic Regression 原理後,我會在下一篇與大家一起學習如何使用Scikit-Learn來實現邏輯迴歸 Logistic Regression
