无限深势井的电子波包模拟
假设我们有一个电子,处于 (0, L) 的一维无限深势井中,初始状态为中心位于 x0 = L2 处的波包:
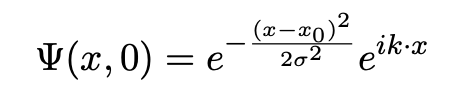
其中 L = 10^(−8)m, σ = 10^(−10)m, k = 5×10^10m^(−1)。
另外物理常数 ̄h = 1.0546 × 10^(−34)J · s,Me = 9.109 × 10^(−31)kg。 设定时间步长 ht = 10^(−18)s,坐标分割数 N = 1000,坐标步长 hx = L/N。
以下模拟是在时间 t = 0, 300ht, 500ht, 800ht, 2000ht 时刻,波函数以及概率密度的分布和变化
代码:
import numpy as np
import matplotlib.pyplot as plt
#设定参数
L = 10.0**(-8)
sgm = 10.0**(-10)
k = 5.0*10**10
hbar = 1.0546*10**(-34)
Me = 9.109*10**(-31)
x0 = L/2
N = 1000
ht = 10.0**(-18)
hx = L/N
a1 = 1 + (1j*hbar*ht)/(2*Me*hx**2)
a2 = -(1j*hbar*ht)/(4*Me*hx**2)
b1 = 1 - (1j*hbar*ht)/(2*Me*hx**2)
b2 = (1j*hbar*ht)/(4*Me*hx**2)
#定义初始波函数
x = np.arange(0,L+hx,hx)
t = np.arange(0,2000*ht+ht,ht)
psi0 = np.exp(-(x-x0)**2/(2*sgm**2))*np.exp(1j*k*x)
#定义中间格点波函数所构成的矩阵
phi = np.zeros((len(psi0), len(t)),dtype=complex)
phi[:,0]=psi0
#定义传递矩阵
A = np.zeros((len(psi0), len(psi0)),dtype=complex)
B = np.zeros((len(psi0), len(psi0)),dtype=complex)
for n in range(len(psi0)):
if n==0:
A[n,0]=a1
A[n,1]=a2
B[n,0]=b1
B[n,1]=b2
elif n==len(psi0)-1:
A[n,n]=a1
A[n,n-1]=a2
B[n,n]=b1
B[n,n-1]=b2
else:
A[n,n-1]=a2
A[n,n]=a1
A[n,n+1]=a2
B[n,n-1]=b2
B[n,n]=b1
B[n,n+1]=b2
#计算中间格点波函数
for n in range(1,len(t)):
phi[:,n]=np.linalg.inv(A) @ B @ phi[:,n-1]
#画图
for m in [0, 300, 500, 800, 2000]:
prob = phi[:,m]*np.conjugate(phi[:,m]) #计算概率分布
lbl='t='+str(m)
plt.figure(1,figsize=(15,3),dpi=300)
plt.plot(x,np.real(phi[:,m]),label=lbl)
plt.xlabel('x')
plt.ylabel('real')
plt.legend()
plt.grid()
plt.figure(2,figsize=(15,3),dpi=300)
plt.plot(x,np.imag(phi[:,m]),label=lbl)
plt.xlabel('x')
plt.ylabel('image')
plt.legend()
plt.grid()
plt.figure(3,figsize=(15,3),dpi=300)
plt.plot(x,np.sqrt(prob),label=lbl)
plt.xlabel('x')
plt.ylabel('probability')
plt.legend()
plt.grid()
输出:
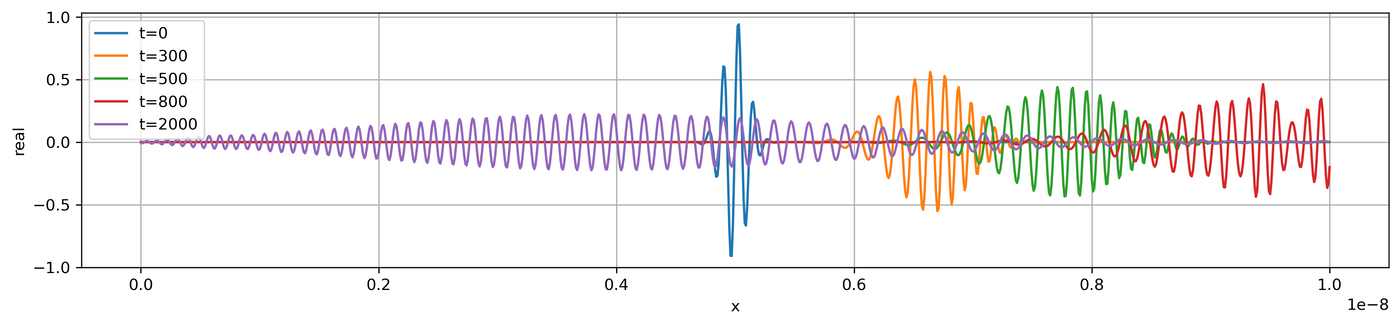
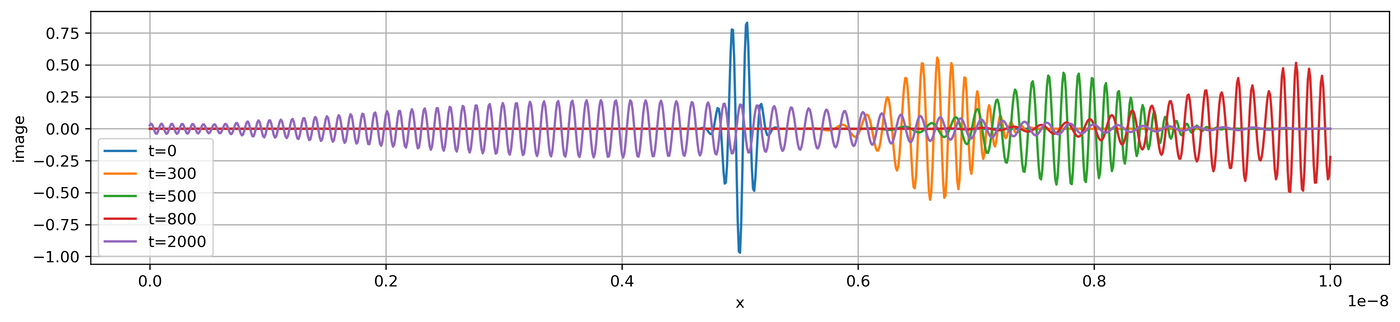
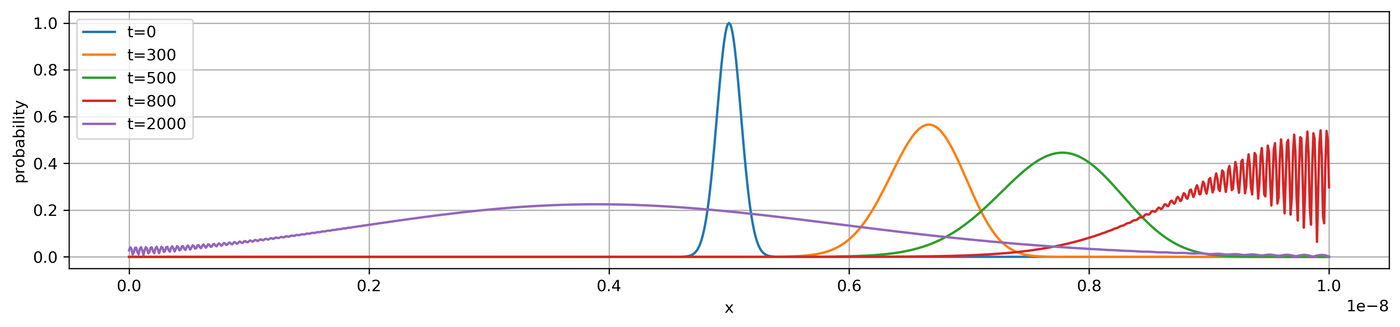
最后需要坦白,跑代码的时间需要大概10分钟,但我还没研究更优化的算法和代码,嗯,因为懒。所以大家谨慎参考。
