姜萍事件是一次提升认知的好机会
认知>学历 智慧>知识

“剩男是被迫单身的,剩女是选择单身的”
向下兼容才会有选择,向上高攀只能变成被选的那个

一個小小的邏輯問題與我無關 與 落後的代價 起跳的木魚
一個小小的邏輯問題 與我無關 與 落後的代價 起跳的木魚 在電影《黑社會2》裏面一位叫鄧伯的黑社會大佬有句很帶感的臺詞“又要賺錢,又不肯出力,留在這又想佔便宜,靠。”我想如果能延伸一下的話,這句話就不只是帶感了,而是赤裸裸地揭開了包括我在內的很多正常人的本性,當然這裏…
一个小小的逻辑问题与我无关 与 落后的代价 起跳的木鱼
一个小小的逻辑问题 与我无关 与 落后的代价 起跳的木鱼 在电影《黑社会2》里面一位叫邓伯的黑社会大佬有句很带感的台词“又要赚钱,又不肯出力,留在这又想占便宜,靠。”我想如果能延伸一下的话,这句话就不只是带感了,而是赤裸裸地揭开了包括我在内的很多正常人的本性,当然这里…
感性和逻辑能共存吗?
黑夜都来了,那么黎明还会远吗?一屋不扫何以扫天下?我们的语境和文化创作中总是有类似的精句,我们知道,文艺创作必定是感性比较充沛,才能让人感同身受。但是把这些来作为人生信条,忽视其背后的上下文,一意孤行地实践。那就好比:“我们的同志85%都是好同志”,那么其推论出来了:“揪出15%来。
马斯克的第一性原理
第一性原理帮助马斯克成就了他的大业
教育的本质与创新的冲突
人们一直在追寻,什么才是好的教育。教育本质上是上一代人希望传承到下一代的最好的东西,但是这个东西缺乏定义,也不断变化。所以人们一直在不断地探索和追求。
真话与好话
喜欢听好话,而不是真话,也许是人性使然,因为小孩子就是这样的。只可惜真话意味着客观事实,你听与不听,他都是真的。不听的人只会影响自己的判断,从而失去对于形势的掌握。
父母与子女世界观冲突下的平衡
随着90后,00后成年参加工作,上一代60后,70后父母与新一代之间关于世界观的冲突,如何平衡,其背后有怎样的缘由?
讀書札記| 一個定義上的邏輯問題
晚上讀Nicolaus Cusanus的De Quaerendo Deum時發現了一個定義分歧引發的邏輯錯誤(貌似)。寫了兩頁草紙論證后發現,啊我就是閑得……

凡人呓语-22.6.6-雨神、幸存者偏差
雨神萧敬腾,是巧合还是真神?

泰利米波斯篇
一篇不那么为人所知的柏拉图对话……
听说你的文章又被批评没逻辑了,可逻辑究竟是个什么玩意儿啊?
要我说,你只要懂了聊天,就懂了什么是logic
职场-为何空降天兵总比内部提拔来的香?
我几时可以加薪、升职机会、更多花红。这是大部分职场人的理想。我几时可以加薪、升职机会、更多花红。这同时也是你上司理想。关于理想,你和上司是达成共识了。但是,你还没跟上司的上司也就是总经理达成任何共识。(1) 张学友(音译)入职公司两年,协助上司掌管公司最大的生意客户。

同样是冲击议会,一次支持,一次反对,但并非双标
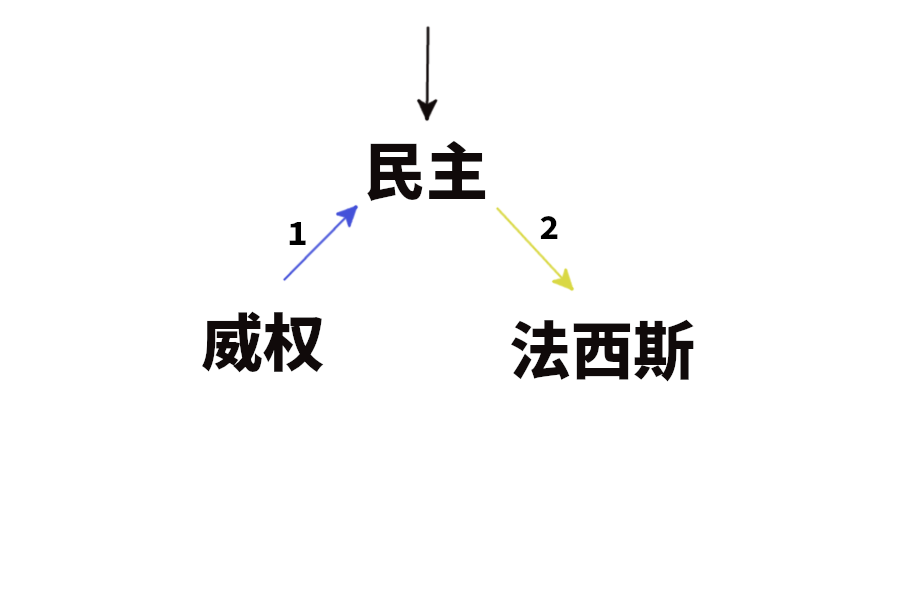
甲:有两个事件,一次是香港抗议者冲击议会,一次是川普支持者冲击议会。同样是冲击议会,你一次支持,一次反对,这是双标。乙:有两个人,一个人给你一杯水要你喝,一个人给你一杯毒药要你喝。同样是给你一杯东西喝,你一次接受,一次拒绝,这是双标。「双标」即「双重标准」,指在本该使用相同标准的...
逻辑谬误
前几天看到一条逻辑谬误的列表,列举了一百六十种常见的逻辑谬误。全文转载:https://telegra.ph/160种逻辑谬误-01-07 这还只是常见的160种:随时有可能有新的逻辑谬误诞生。看到这样的帖子,我意识到了一个重要的问题: 逻辑根本不适合用来思考。

捍卫马克思4:给所有曲解马克思的人(马克思哲学、经济学通俗讲义4)
八、形式逻辑、辨证逻辑、现实逻辑 逻辑的本质是关系间的某种组合方式。例如在形式逻辑里,排中律意味着命题和它的反命题之间的关系被一种绝对的组合方式联系在一起,就是它们不能同时为真。而没有命题之间的关系,所谓的逻辑规则也是不存在的。在形式逻辑的发展初期,人们觉得逻辑规则是绝对的、甚至...
从汉隆剃刀谈起
各种定律法则数不胜数,比如“墨菲定律”,“帕金森定律”,这些都不是科学定理,也无法严格证明,但是这些可以看作是认知模型。最近看到一个特别有意思的定律叫“汉隆剃刀(Hanlon's Razor)”,最早被称作“墨菲定律版的奥卡姆剃刀法则”。不过根本不需要了解什么是墨菲定律,也不需要...
名人名言论证法
从小学开始,老师就会教导我们写作文的时候要多引用名人名言来论证自己的观点,于是读书少的我们为了强行凑名人名言,就开始自己发明名人名言。随便自己编一段自以为很有哲理的话,然后冠上一个名人的名字,例如鲁迅。网上一个很流行的meme就是配上一张鲁迅的图片再加上一句很不名人名言的话,来取笑随便发明名人名言的人。
回到粗糙的地面:我讀書的三大原則
我们在光滑的冰面上,这里没有摩擦,因此,在一定意义上,这种条件是理想的,但也正因为此,我们不能行走:所以,我们需要摩擦。回到粗糙的地面上吧。——维特根斯坦 关于读书,杨绛先生说过一句话:“你的问题是读书太少,想得太多”,这曾在朋友圈广为流传,自有一定的道理。